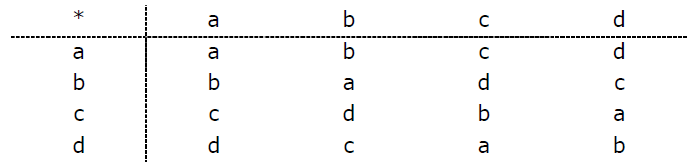
Which one of the following choices is correct?
(A) a, b are generators (B) b, c are generators
(C) c, d are generators (D) d, a are generators
Q.1. Which one of the following in NOT necessarily a property of a Group?
(A) Commutativity
(B) Associativity
(C) Existence of inverse for every element
(D) Existence of identity
Sol : By definition, in a group, commutativity is not necessary. So option (A) is correct.
Q.2. What is the chromatic number of an n-vertex simple connected graph which does
not contain any odd length cycle? Assume n ≥2.
(A) 2
(B) 3
(C) n-1
(D) n
Sol : Chromatic number of a graph is the minimum number of colors required to color all vertices such that no two adjacent vertices are colored with same color. Since here we have no odd cycle, we can color whole graph with only 2 colors, coloring the vertices with alternate colors. So option (A) is correct.
Q.3. Which one of the following is TRUE for any simple connected undirected graph
with more than 2 vertices?
(A) No two vertices have the same degree.
(B) At least two vertices have the same degree.
(C) At least three vertices have the same degree.
(D) All vertices have the same degree.
Sol : We argue that "At least two vertices have the same degree". Let us see why. If that is not true i.e. if all n vertices
have different degrees, then degrees must be 0,1,2...,n-1, we can't have a degree > n-1, because there are only n vertices and graph
is simple i.e. has no self loops.
But this degree sequence 0,1,2,...,n-1 is not possible, because it means there is a vertex with 0 degree (not connected to any
vertex), and there is a vertex with n-1 degree (connected to every vertex), which is not possible simultaneously.
So option (B) is correct.
Q.4. Consider the binary relation R = {(x,y), (x,z), (z,x), (z,y)} on the set {x,y,z}.
Which one of the following is TRUE?
(A) R is symmetric but NOT antisymmetric
(B) R is NOT symmetric but antisymmetric
(C) R is both symmetric and antisymmetric
(D) R is neither symmetric nor antisymmetric
Sol : A relation is symmetric if, for each (x,y) in R, (y,x) is also in R. This relation R in question is not symmetric,
because for (x,y), R doesn't have (y,x).
A relation is antisymmetric if, for each pair of (x,y) and (y,x) in R, x=y. Here R in question is not antisymmetric because for
pairs (x,z) and (z,x), x ≠ z.
So option (D) is correct.
Q.21. An unbalanced dice (with 6 faces, numbered from 1 to 6) is thrown. The
probability that the face value is odd is 90% of the probability that the face value
is even. The probability of getting any even numbered face is the same.
If the probability that the face is even given that it is greater than 3 is 0.75,
which one of the following options is closest to the probability that the face value
exceeds 3?
(A) 0.453
(B) 0.468
(C) 0.485
(D) 0.492
Sol : Let P(even) = x, so P(odd) = 90% of x = 9x/10, but P(even) + P(odd) = 1, so x + 9x/10 = 1, so x = 10/19.
So P(even) = 10/19. Also since prob of any even number is same, so P(2) = P(4) = P(6) = 10/(19*3) = 10/57
Now P(even and exceeds 3) = P(exceeds 3) * P(even|exceeds). We have to evaluate P(exceeds 3), so
P(exceeds 3) = P(even and exceeds 3)/P(even|exceeds) = (P(4) + P(6))/0.75 = (20/57)/0.75 = 0.468
So option (B) is correct.
Q.22. For the composition table of a cyclic group shown below
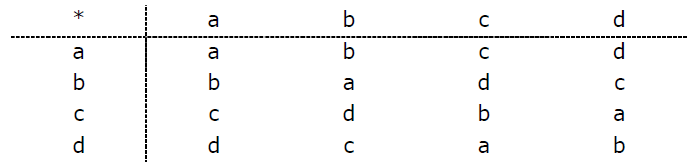
Which one of the following choices is correct?
(A) a, b are generators
(B) b, c are generators
(C) c, d are generators
(D) d, a are generators
Sol : An element is a generator for a cyclic group if on repeated applications of it upon itself, it can generate all
elements of group.
For example here : a*a = a, then (a*a)*a = a*a = a, and so on. Here we see that no matter how many times we apply a on itself,
we can't generate any other element except a, so a is not a generator.
Now for b, b*b = a. Then (b*b)*b = a*b = b. Then (b*b*b)*b = b*b = a, and so on. Here again we see that we can only generate a and b
on repeated application of b on itself. So it is not a generator.
Now for c, c*c = b. Then (c*c)*c = b*c = d. Then (c*c*c)*c = d*c = a. Then (c*c*c*c)*c = a*c = c. So we see that we have generated
all elements of group. So c is a generator.
For d, d*d = b. Then (d*d)*d = b*d = c. Then (d*d*d)*d = c*d = a. Then (d*d*d*d)*d = a*d = d. So we have generated all elements
of group from d, so d is a generator.
So c and d are generators. So option (C) is correct.
Q.23. Which one of the following is the most appropriate logical formula to represent
the statement? $``$Gold and silver ornaments are precious$''$.
The following notations are used:
G(x): x is a gold ornament
S(x): x is a silver ornament
P(x): x is precious
(A) ∀x(P(x) → (G(x) ∧ S(x)))
(B) ∀x((G(x) ∧ S(x)) → P(x))
(C) ∃;x((G(x) ∧ S(x)) → P(x))
(D) ∀x((G(x) ∨ S(x)) → P(x))
Sol : Basically statement is saying that for every thing, if it is a Gold ornament or a silver ornament, then it is precious.
So ∀x((G(x) ∨ S(x)) → P(x)) is correct logical formula, and therefore option (D) is correct.
Q.24. The binary operation □ is defined as follows
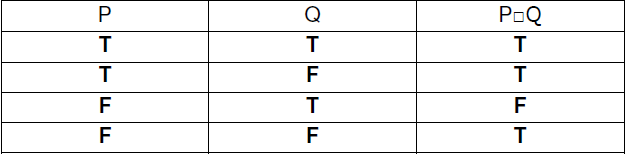
(A) ¬Q□¬P
(B) P□¬Q
(C) ¬P□Q
(D) ¬P□¬Q
Sol : If we compare column of P□Q in table with P ∨ Q, we need both F in 3rd row of table, and for that we need ¬Q instead of Q. So P ∨ Q is equivalent to P□¬Q, and therefore, option (B) is correct.
Q.25. $\int^{\pi/4}_0 (1-tanx)/(1+tanx)\,dx $
(A) 0
(B) 1
(C) ln 2
(D) 1/2ln 2
Sol : We know that (1-tanx)/(1+tanx) = tan(π/4 - x), so $$\int^{\pi/4}_0 (1-tanx)/(1+tanx)\,dx = \int^{\pi/4}_0 tan(π/4 - x)\,dx = -\left[\ln \sec(\pi/4 - x)\right]^{\pi/4}_0 = 1/2 \ln 2$$ So option (D) is correct.
Q.26. Consider the following well-formed formulae:
I. ¬∀x(P(x))
II. ¬∃x(P(x))
III. ¬∃x(¬P(x))
IV. ∃x(¬P(x))
Which of the above are equivalent?
(A) I and III
(B) I and IV
(C) II and III
(D) II and IV
Sol : A formula ∀x(P(x)) is equivalent to formula ¬∃x(¬P(x)) i.e. add ¬ inside and outside, and
convert ∀ to ∃.
So, ¬∀x(P(x)) is equivalent to ∃x(¬P(x)). So option (B) is correct.