Sol : There are multiple ways to find rank of matrix. For this question, simplest way is to see that two rows are not independent, 2nd is scalar multiple of 1st. So here we have only one independent row, and thus rank is 1, so option (C) is correct.
Q.1.2 The trapezoidal rule for integration gives exact result when the integrand is a polynomial of degree
(a) 0 but not 1 (b) 1 but not 0
(c) 0 or 1 (d) 2
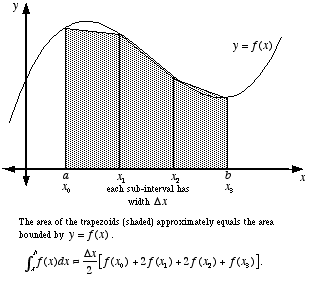
Sol : In trapezoidal rule, we estimate the definite integral of a function by breaking area under it into many smaller trapezoids as shown below.

Now as we can see, some trapezioids don't fit completely into this curve, so there is an error associated. But if the curve is of constant function i.e. parallel to x-axis, then all trapezoids will fit completely (infact they will become rectangles), so that would be error free. Similarly, if curve is of function of degree 1, then curve will be a straight line, and in that case also, all trapezoids will fit completely. So there is no error in degree 1 also. So option (c) is correct.
Q.1.6. Which of the following is true?
(A) The set of all rational negative numbers A group G should follow 4 properties :
(B) The set of all non-singular matrices forms a group under multiplication.
(C) The set of all matrices forms a group under multiplication.
(D) Both B and C are true
Sol : A group G should follow 4 properties :
Q.1.8 "If X then Y unless Z" is represented by which of the following formulas in propositional logic? ("\(\neg\), is negation, "\(\wedge\)", is conjunction, and "\(\to\)" is implication)
(a) (X\(\wedge\neg\)Z)\(\to\)Y (b) (X\(\wedge\)Y)\(\to\neg\)Z (c) X\(\to\)(Y\(\wedge\neg\)Z) (d) (X\(\to\)Y)\(\wedge\neg\)Z
Sol : The statement "If X then Y unless Z" means, if Z doesn't occur, X implies Y i.e. \(\neg\)Z\(\to\)(X\(\to\)Y), which is equivalent to Z\(\vee\)(X\(\to\)Y) (since P\(\to\)Q ≡ \(\neg\)P\(\vee\)Q), which is then equivalent to Z\(\vee\)(\(\neg\)X\(\vee\)Y). Now we can look into options which one matches with this.
So option (a) is (X\(\wedge\neg\)Z)\(\to\)Y = \(\neg\)((X\(\wedge\neg\)Z))\(\vee\)Y = (\(\neg\)X\(\vee\)Z)\(\vee\)Y, which matches our expression. So option a is correct.
Q.2.15. The Newton-Raphson iteration \(X_{n+1}=\frac{X_n}{2} + \frac{3}{2X_n}\) can be used to solve the equation
(a) \(X^2 = 3\) (b) \(X^3 = 3\)
(c) \(X^2 = 2\) (d) \(X^3 = 2\)
Sol : Newton-Raphson method is used to find roots of a function f(x) i.e. values of x, where f(x) = 0.
In this, we start with an initial guess of x, and correct it in successive iterations.
So let our guess at some point of time is \(x_n\), so then function value is \(f(x_n)\) and we want a better \(x_{n+1}\) for next iteration.
Now we draw tangent from point \((x_n,f(x_n))\), which cuts off x-axis at \(x_{n+1}\). This will be our next guess. So we want to find this intersection point \(x_{n+1}\). We know \(f'(x_n) = \) slope of tangent \( = \frac{f(x_n) - 0}{x_n - x_{n+1}}\).
So we get \(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\)
So we try to bring given equation in above form. Given equation is : $$x_{n+1} = \frac{x_n}{2}+\frac{3}{2x_n} = x_n - \frac{x_n}{2}+\frac{3}{2x_n} = x_n - \frac{x_n^2-3}{2x_n}$$ So clearly $f(x) = x^2 - 3$, so root of f(x) means $x^2 - 3 = 0$ i.e. we are trying to find square root of 3. so option (a) is correct.
Q.2.16. Four fair coins are tossed simultaneously. The probability that at least one head and one tail turn up is
(a) 1/16 (b) 1/8
(c) 7/8 (d) 15/16
Sol : Only cases where specified condition is not met are : HHHH, and TTTT. In all other cases, we have atleast one head and one tail. So P = 14/16 = 7/8. So option (c) is correct. Also see Q.2.4 (2001)
Q.2.17. The binary relation S = \(\phi\) (empty set) on set A = {1,2,3} is
(a) Neither reflexive nor symmetric (b) Symmetric and reflexive (c) Reflexive and transitive (d) Transitive and symmetric
Sol :