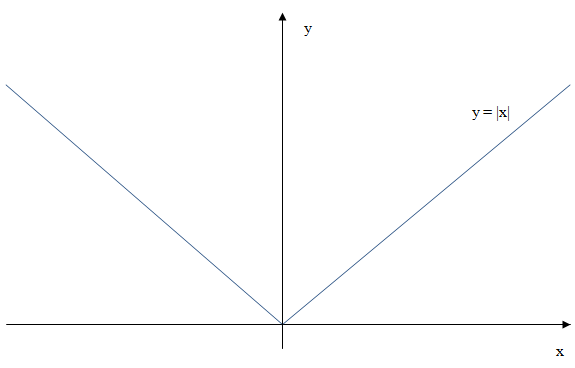
Q.1. Consider the following two statements about the function $f(x)=\left\vert x\right\vert$:
P. $f(x)$ is continuous for all real values of $x$.
Q. $f(x)$ is differentiable for all real values of $x$ .
Which of the following is TRUE?
(A) P is true and Q is false.
(B) P is false and Q is true.
(C) Both P and Q are true.
(D) Both P and Q are false.
Sol : Below is the graph of the function $f(x)=\left\vert x\right\vert$ :

Clearly, this function is continuous for all real values, but due to sharp point at $x=0$, this function is not differentiable at $x=0$. So option (A) is correct.
Q.2. Let S be a set of n elements. The number of ordered pairs in the largest and the
smallest equivalence relations on S are:
(A) n and n
(B) $n^2$ and n
(C) $n^2$ and 0
(D) n and 1
Sol : In largest equivalence relation, all $n^2$ ordered pairs will come.
In smallest, only n diagonal pairs i.e. pairs
of type (a,a) will come. Note that this is an equivalence relation, because it is reflexive, symmetric and transitive. Moreover,
we can't get smaller equivalence relation than this because we must include at least diagonal elements to make it reflexive.
So option (B) is correct.
Q.3. What is the maximum number of different Boolean functions involving n Boolean
variables?
(A) $n^2$
(B) $2^n$
(C) $2^{2^n}$
(D) $2^{n^2}$
Sol : Since we have n boolean variables, we will have $2^n$ entries in truth table. Now each result entry i.e. a function applied to a string of n 0s and 1s, can be true or false. So for each of the $2^n$ result entries, we have 2 choices. So total no. of functions are $2^{2^n}$. So option (C) is correct.
Q.4. Let G be the non-planar graph with the minimum possible number of edges. Then
G has
(A) 9 edges and 5 vertices
(B) 9 edges and 6 vertices
(C) 10 edges and 5 vertices
(D) 10 edges and 6 vertices
Sol : We know that $K_5$ (which has 10 edges and 5 vertices) and $K_{3,3}$ (which has 9 edges and 6 vertices) are non-planar graphs.
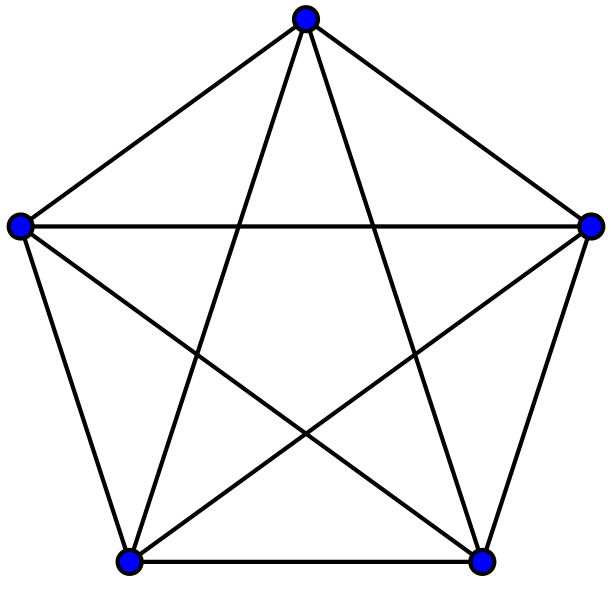

Since we are asked about minimum number of edges, answer should be $k_{3,3}$ i.e. option (B) is correct.
Q.21. How many different non-isomorphic Abelian groups of order 4 are there?
(A) 2
(B) 3
(C) 4
(D) 5
Sol : Number of non-isomorphic Abelian groups of order n can be calculated as follows :
Q.22. Let Graph(x) be a predicate which denotes that x is a graph. Let Connected(x) be
a predicate which denotes that x is connected. Which of the following first order
logic sentences DOES NOT represent the statement: "Not every graph is
connected"?
(A) ¬∀x(Graph(x) ⇒ Connected(x))
(B) ∃x(Graph(x) ∧ ¬Connected(x))
(C) ¬∀x(¬Graph(x) ∨ Connected(x))
(D) ∀x(Graph(x) ⇒ ¬Connected(x))
Sol : "Not every graph is connected" means that "there exists a graph which is not connected", which we can write as
∃x(Graph(x) ∧ ¬Connected(x)), so option (B) represents given statement.
Now ∃x(f(x)) is equivalent to ¬∀x(¬f(x)).
So ∃x(Graph(x) ∧ ¬Connected(x)) is equivalent to ¬∀x(¬(Graph(x) ∧ ¬Connected(x))), which
we can simplify as ¬∀x(¬Graph(x) ∨ Connected(x)), so option (C) also represents given statement.
Moreover, we can rewrite option (C) as ¬∀x(Graph(x) ⇒ Connected(x)), so option (A)
also represents given statement.
So option (D) doesn't represent given statement. so answer is option (D).
Q.23. Which of the following graphs has an Eulerian circuit?
(A) Any k-regular graph where k is an even number.
(B) A complete graph on 90 vertices.
(C) The complement of a cycle on 25 vertices.
(D) None of the above
Sol : So there are two conditions to identify if a graph has an Eulerian circuit :
Q.24. Suppose we uniformly and randomly select a permutation from the 20!
Permutations of 1, 2, 3 ... ,20. What is the probability that 2 appears at an
earlier position than any other even number in the selected permutation?
(A) 1/2
(B) 1/10
(C) 9!/20!
(D) None of these
Sol : Here order of odd numbers doesn't matter, so we focus only on 10 even numbers as if we have to arrange only 10 even numbers . In general, digit 2 can be placed at any of the 10 places available, but according to question, 2 can be placed at only 1st because it has to appear before every other even number. So out of 10 choices, we have only 1 favourable choice, so probability is 1/10. So option (B) is correct.
Q.25. Let A be a 4 * 4 matrix with eigenvalues -5, -2, 1, 4. Which of the following is an
eigenvalue of $\left( \begin{array}{cc}
A & I \\
I & A \end{array} \right)$, where I is the 4 * 4 identity matrix?
(A) -5
(B) -7
(C) 2
(D) 1
Sol : Let us call given matrix as B. We can find its eigenvalues by solving it characteristic equation.
Characteristic equation of B is given by :
$$ \left\vert \begin{array}{cc}(A-λI) & I \\I & (A-λI) \end{array} \right\vert = 0$$
Now by using properties of block matrix according to
http://en.wikipedia.org/wiki/Determinant#Block_matrices
$$ \left\vert(A-λI)^2 - I^2\right\vert = 0 \Rightarrow \left\vert(A - (λ-1)I)*(A - (λ+1)I)\right\vert
= 0$$
We know that |A*B| = |A| * |B|, so using that,
$$ \left\vert(A - (λ-1)I)\right\vert*\left\vert(A - (λ+1)I)\right\vert = 0$$
So either
$$
\left\vert(A - (λ-1)I)\right\vert = 0
$$
or
$$
\left\vert(A - (λ+1)I)\right\vert=0
$$
Also if $λ_A$ is eigen value of A, then we have $\left\vert(A - λ_AI)\right\vert = 0$, so by comparing this
equation, with above 2 equations, we get either $λ-1 = λ_A$ or $λ+1 = λ_A$ i.e. either
$λ = λ_A + 1$ or $λ = λ_A - 1$.
Since we are already given $λ_A = {-5,-2,1,4}$, we get $λ = {-4,-1,2,5,-6,-3,0,3}$. So only eigenvalue 2 matches
from options, so option (C) is correct.
Q.26. Consider the set $S = \{ a , b , c , d \}$ . Consider the following 4 partitions $π_1,π_2,π_3,π_4$ on $S : π_1 = \{\overline{abcd}\} , π_2 = \{\overline{ab}, \overline{cd}\}, π_3 = \{\overline{abc}, \overline{d}\}, π_4 = \{\bar{a}, \bar{b}, \bar{c}, \bar{d}\}$. Let $p$ be the partial order on the set of partitions $S' = \{π_1,π_2,π_3,π_4\}$ defined as follows: $π_i \;p\; π_j$ if and only if $π_i$ refines $π_j$. The poset diagram for $(S', p)$ is:

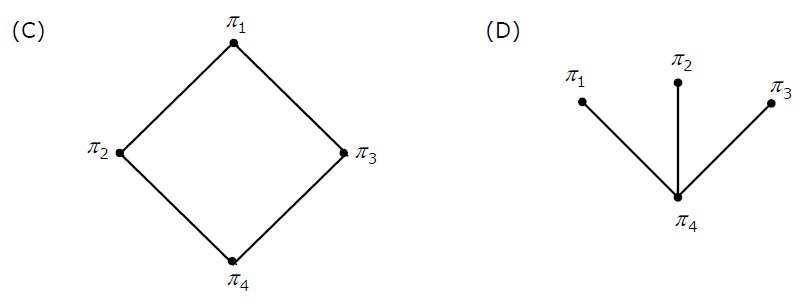
Sol : $π_i$ refines $π_j$ means every element of $π_i$ is a subset of some element of $π_j$. So $π_4$
refines every partition. So it has to be at the bottom of poset diagram. Moreover, neither $π_2$ refines $π_3$, nor
$π_3$ refines $π_2$. Also $π_1$ is refined by every set, so it has to be at the top.
Only option (C) satisfies all the above properties, so it is the correct answer.
Q.27. Consider the set of (column) vectors defined by
$X = \{x \in R^3 \vert x_1 + x_2 + x_3 = 0, \text{where} x^T = [x1,x2,x3]^T\}$. Which of the following is TRUE ?
(A) $\{[1,-1,0]^T,[1,0,-1]^T\}$ is a basis for the subspace $X$.
(B) $\{[1,-1,0]^T,[1,0,-1]^T\}$ is a linearly independent set, but it does not span $X$ and
therefore is not a basis of $X$
(C) $X$ is not a subspace of $R^3$.
(D) None of the above
Sol : A set of vectors $X$ is a subspace of a space if it satisfies following properties :
Now let us see whether vector set $S = \{[1,-1,0]^T,[1,0,-1]^T\}$ is a basis for subspace $X$ or not. Clearly vectors in $S$ are linearly independent, because one vector is not scalar multiple of other. Moreover, every vector in $X$ can be obtained by a linear combination of vectors in $S$. Let us see why.
Suppose we have a vector $[x_1,x_2,x_3]^T$ in $X$, and let linear combination which gives us this vector is $a*[1,-1,0]^T+b*[1,0,-1]^T$. So we have $$a+b = x_1, -a = x_2, -b = x_3$$ So if we put $a=-x_2$, and $b=-x_3$, we will get $a+b = -x_2 - x_3 = x_1$ i.e. $x_1+x_2+x_3 = 0$, which satisfies property of $X$. So $S$ is a basis for $X$. So option (A) is correct.
Q.28. Consider the series $x_{n+1} = \frac{x_n}{2}+\frac{9}{8x_n},x_0 = 0.5$ obtained from the Newton-Raphson
method. The series converges to
(A) 1.5
(B) $\sqrt{2}$
(C) 1.6
(D) 1.4
Sol : Let us see which function's root is found using given series. We know that, according to Newton-Raphson method,
$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$
So we try to bring given equation in above form. Given equation is :
$$x_{n+1} = \frac{x_n}{2}+\frac{9}{8x_n} = x_n - \frac{x_n}{2}+\frac{9}{8x_n} = x_n - \frac{4x_n^2-9}{8x_n}$$
So clearly $f(x) = 4x^2 - 9$. We know its roots are $\pm\frac{3}{2} = \pm 1.5$, but if we start from $x_0 = 0.5$, according to
equation, we cannot get negative value at any time, so answer is 1.5 i.e. option (A) is correct.
See also Q.2.15 (2002), Q.42 (2003), Q.2 (2010) and Q.22 (2008).
Q.33. Define the connective * for the Boolean variables X and Y as: X * Y = XY + X'Y'.
Let Z = X * Y. Consider the following expressions P, Q and R.
$P : X = Y * Z, Q :Y = X * Z, R : X *Y * Z = 1$
Which of the following is TRUE?
(A) Only P and Q are valid.
(B) Only Q and R are valid.
(C) Only P and R are valid.
(D) All P, Q, R are valid.
Sol : Let us construct truth table for all the expressions given in question :
| X | Y | Z | Y*Z | X*Z | X*Y*Z |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Q.84. Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move
either one unit up or one unit right, i.e., if it is at $(i,j)$ then it can move to either
$(i + 1, j)$ or $(i,j + 1)$.
How many distinct paths are there for the robot to reach the point (10,10)
starting from the initial position (0,0)?
(A) $^{20}\mathrm{C}_{10}$
(B) $2^{20}$
(C) $2^{10}$
(D) None of the above.
Sol : At each move, robot can move either 1 unit right, or 1 unit up, and there will be 20 such moves required to reach (10,10) from (0,0). So we have to divide these 20 moves, numbered from 1 to 20, into 2 groups : right group and up group. Right group contains those moves in which we move right, and up group contains those moves in which we move up. Each group contains 10 elements each. So basically, we have to divide 20 things into 2 groups of 10 10 things each, which can be done in $\frac{20!}{10!*10!} = ^{20}\mathrm{C}_{10}$ ways. So option (A) is correct.
Q.85. Suppose that the robot is not allowed to traverse the line segment from (4,4) to
(5,4). With this constraint, how many distinct paths are there for the robot to
reach (10,10) starting from (0,0)?
(A) $2^9$
(B) $2^{19}$
(C) $^{8}\mathrm{C}_{4}*^{11}\mathrm{C}_{5}$
(D) $^{20}\mathrm{C}_{10} - ^{8}\mathrm{C}_{4}*^{11}\mathrm{C}_{5}$
Sol : Since we are not allowed to traverse from (4,4) to (5,4). So we will subtract all those paths which were paasing through
(4,4) to (5,4).
To count number of paths passing through (4,4) to (5,4), we find number of paths from (0,0) to (4,4), and then from (5,4) to (10,10).
From (0,0) to (4,4), number of paths = $^{8}\mathrm{C}_{4}$ (found in same way as in previous question).
From (5,4) to (10,10), number of paths = $^{11}\mathrm{C}_{5}$.
So total number of paths required : $^{20}\mathrm{C}_{10} - ^{8}\mathrm{C}_{4}*^{11}\mathrm{C}_{5}$.
So option (D) is correct.