So option (C) is correct.
Q.1. Consider the polynomial $p(x) = a_0 + a_1x + a_2x^2 + a_3x^3$ , where $a_i ≠0\; ∀i$. The minimum number of
multiplications needed to evaluate p on an input x is:
(A) 3
(B) 4
(C) 6
(D) 9
Sol : We can use just horner's method, according to which, we can write p(x) as :
$$p(x) = a_0 + x(a_1 + x(a_2 + a_3x))$$
So as we can see, here we need only 3 multiplications, so option (A) is correct.
Note that in question paper, $a_3x^2$ is written instead of $a_3x^3$, but for $a_3x^2$, answer is 2, because we can save
one more multiplication between $a_3$ and x, but 2 is not in the options, so i guess question paper had a printing mistake.
Q.2. Let X,Y,Z be sets of sizes x, y and z respectively. Let W = X * Y and E be the set of all subsets of W.
The number of functions from Z to E is:
(A) $z^{2^{xy}}$
(B) $z * 2^{xy}$
(C) $z^{2^{x+y}}$
(D) $2^{xyz}$
Sol : Number of functions from a set A of size m to set B of size n is $n^m$, because each of the m elements of A has
n choices for mapping. Now here $m = |Z| = z$, and $n = |E| = 2^{xy}$ because number of subsets of a set of size n is $2^n$,
and here set W has size of $xy$.
So number of functions from Z to E = $(2^{xy})^z = 2^{xyz}$. So option (D) is correct.
Q.3. The set {1,2,3,5,7,8,9} under multiplication modulo 10 is not a group. Given below are four plausible reasons.
Which one of the m is false?
(A) It is not closed
(B) 2 does not have an inverse
(C) 3 does not have an inverse
(D) 8 does not have an inverse
Sol : Let us go through each option :
Q.4. relation R is defined on ordered pairs of integers as follows:
$$(x,y)R(u,v) \text{ if } x<u \text{ and } y>v$$ Then R is:
(A) Neither a Partial Order nor an Equivalence Relation
(B) A Partial Order but not a Total Order
(C) A total Order
(D) An Equivalence Relation
Sol : A relation R is partial Order iff it is reflexive, antisymmetric, and transitive.
A relation R is Equivalence Relation iff it is reflexive, symmetric, and transitive, but we have already seen that R is not reflexive, so R is not Equivalence relation.
So option (A) is correct.
Q.18. We are given a set $X = {x_1 , \cdots x_n }$ where $x_i = 2^i$ . A sample S ⊆ X is drawn by selecting each $x_i$
independently with probability $p_i = \frac{1}{2}$. The expected value of the smallest number in sample S is:
(A) 1/n
(B) 2
(C) $\sqrt{n}$
(D) n
Sol : So we have a set $X = \{2,4,\cdots,2^n\}$. We select a subset S of X.
We know that $E[X] = \sum$ XP(X). In this question, random variable X is value of smallest number in S, so X can take value
from ${2,4,\cdots,2^n}$.
So E[smallest number] = $\sum \limits_{i=1}^{n} X_i*\text{P}(X_i \text{ is smallest })$.
Now P($X_i$ is smallest = $\left(\frac{1}{2}\right)^i$, because for $X_i$ to be smallest, $X_1, X_2,\cdots,X_{i-1}$ must not be selected (which has probability $\frac{1}{2^{i-1}}$), and $X_i$ must be selected, which has probability $\frac{1}{2}$ (that will guarantee that $X_i$ is smallest in a subset S)
Q.21. For each element in a set of size $2n$, an unbiased coin is tossed. The $2n$ coin tosses are independent.
An element is chosen if the corresponding coin toss were head. The probability that exactly $n$ elements
are chosen is
(A) $\frac{^{2n}\mathrm{C}_n}{4^n}$
(B) $\frac{^{2n}\mathrm{C}_n}{2^n}$
(C) $\frac{1}{^{2n}\mathrm{C}_n}$
(D) $\frac{1}{2}$
Sol : This can be done using binomial theorem, it is just asking probability of $n$ heads out of $2n$ coin tosses. So $$\text{P} = \; ^{2n}\mathrm{C}_n*\left(\frac{1}{2}\right)^n*\left(\frac{1}{2}\right)^n = \frac{^{2n}\mathrm{C}_n}{4^n}$$ So option (A) is correct.
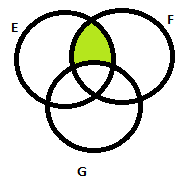
Q.22. Let E, F and G be finite sets.
Let X = (E ∩ F) - (F ∩ G) and Y = (E - (E ∩ G)) - (E - F).
Which one of the following is true?
(A) X ⊂ Y
(B) X ⊃ Y
(C) X = Y
(D) X - Y ≠ φ and Y - X ≠ φ
Sol : If we draw the venn diagrams of both X and Y, we find that both cover exactly same region (shown in gigure below).

So option (C) is correct.
Q.23. F is an n*n real matrix. b is an n*1 real vector. Suppose there are two n*1 vectors, u and v such that, u ≠ v and Fu = b, Fv = b.
Which one of the following statements is false?
(A) Determinant of F is zero.
(B) There are an infinite number of solutions to Fx = b
(C) There is an x≠0 such that Fx = 0
(D) F must have two identical rows
Sol : Since Fu = b, and also Fv = b, so we have (Fu - Fb) = 0 i.e. F(u-v) = 0. Since u≠v, F is a singular matrix i.e. its determinant is 0.
Now for a singular matrix F, either Fx = b has no solution or infinitely many solutions, but as we are already given two solutions u and v for x, Fx = b has to have
infinitely many solutions.
Moreover, by definition of singular matrix, there exists an x≠0 such that Fx = 0 .
So options (A), (B), and (C) are true. Option (D) is false because it may not be necessary that two rows are identical, instead, two columns can be identical
and we can get F as singular matrix then.
So option (D) is correct answer.
Q.24. Given a set of elements N = {1, 2, ..., n} and two arbitrary subsets A⊆N and B⊆N, how many of the
n! permutations $\pi$ from N to N satisfy min($\pi$(A)) = min($\pi$(B)), where min(S) is the smallest integer in
the set of integers S, and $\pi$(S) is the set of integers obtained by applying permutation $\pi$ to each element of S?
(A) (n - |A ∪ B|) |A| |B|
(B) $(|A|^2 + |B|^2)n^2$
(C) $n! \frac{|A ∩ B|}{|A ∪ B|}$
(D) $\frac{|A ∩ B|^2}{^n \mathrm{C}_{|A ∪ B|}}$
Sol : First let us understand what question is asking. So $\pi$ is a function from N to N, which just permutes the elements of N, so there will be n! such permutations.
Now given a particular $\pi$ i.e. given a particular permutation scheme, we have to find number of permutations out of these n! permuations in which minimum elements of A and B
after applying $\pi$ to them are same.
So for example, if N = {1,2,3}, $\pi$ is {2,3,1}, and if A is {1,3}, then $\pi$(A) = {2,1}.
Now number of elements in A ∪ B is |A ∪ B|. We can choose permutations for A ∪ B in $^n\mathrm{C}_{|A∪B|}$ ways. Note that here we are just choosing elements for permutation,
and not actually permuting. Let this chosen set be P. Now once we have chosen numbers for permutations, we have to select mapping from each element of A ∪ B to some element of P.
So first of all, to achieve required condition specified in question, we have to map minimum number in P to any of the number in A ∩ B, so that min($\pi$(A)) = min($\pi$(B)). We can
do this in |A∩B| ways, since we can choose any element of |A∩B| to be mapped to minimum number in P.
Now we come to permutation. We can permute numbers in P in |A∪B-1|! ways, since one number (minimum) is already fixed.
Moreover, we can also permute remaining n - |A∪B-1| in (n - |A∪B-1|)! ways, so total no. of ways =
$$ ^n\mathrm{C}_{|A∪B|} * |A∩B| * |A∪B-1|! * (n - |A∪B-1|)! = n! \frac{|A ∩ B|}{|A ∪ B|}$$
So option (C) is correct.
Note : Some answer keys on web have shown answer as option (D), which is clearly incorrect. Suppose |A ∪ B| = 3, and |A ∩ B| = 1, and n = 4, then option (D)
evaluates to $\frac{1}{4} = 0.25$, which doesn't make sense.
Q.25. Let $S = \{1,2,3,...,m\},m>3$. Let $X_1,X_2,...X_n$ be subsets of S each of size 3. Define a function $f$ from $S$ to the set of natural numbers as,
$f(i)$ is the number of sets $X_j$ that contain the element $i$. That is $f(i) = \left\vert\{j|i\in X_j\}\right\vert$.
Then $\sum\limits_{i=1}^{m} f(i)$ is :
(A) 3m
(B) 3n
(C) 2m+1
(D) 2n+1
Sol : First of all, number of subsets of S of size 3 is $^m\mathrm{C}_3$ i.e. $n=^m\mathrm{C}_3$. Now we count number of subsets in which a particular element $i$ appears, that will be
$^{m-1}\mathrm{C}_2$, because 1 element is already known, and we have to choose 2 elements from remaining m-1 elements.
So
$$\sum\limits_{i=1}^{m} f(i) = m * ^{m-1}\mathrm{C}_2 = 3 * ^m\mathrm{C}_3 = 3n$$
So option (B) is correct.
Q.26. Which one of the first order predicate calculus statements given below correctly expresses the following English statement?
Tigers and lions attack if they are hungry or threatened.
(A) ∀x[(tiger(x) ∧ lion(x)) → {(hungry(x) ∨ threatened(x)) → attacks(x)}]
(B) ∀x[(tiger(x) ∨ lion(x)) → {(hungry(x) ∨ threatened(x)) ∧ attacks(x)}]
(C) ∀x[(tiger(x) ∨ lion(x)) → {attacks(x) → (hungry(x) ∨ threatened(x))}]
(D) ∀x[(tiger(x) ∨ lion(x)) → {(hungry(x) ∨ threatened(x)) → attacks(x)}]
Sol : The statement "Tigers and lions attack if they are hungry or threatened" means that if an animal is either tiger or
lion, then if it is hungry or threatened, it will attack. So option (D) is correct.
Don't get confused by "and" between tigers and lions in the statement. This "and" doesn't mean that we will write "tiger(x) ∧ lion(x)
", because that would have meant that an animal is both tiger and lion, which is not what we want.
Q.27. Consider the following propositional statements:
P1 : ((A ∧ B) → C)) ≡ ((A → C) ∧ (B → C))
P2 : ((A ∨ B) → C)) ≡ ((A → C) ∨ (B → C))
Which one of the following is true?
(A) P1 is a tautology, but not P2
(B) P2 is a tautology, but not P1
(C) P1 and P2 are both tautologies
(D) Both P1 and P2 are not tautologies
Sol : The easiest way to solve this question by creating truth tables for the expressions given. Note that P1 will be a tautology if truth table for left expression is exactly same as truth table for right expression. Same holds for P2 also.
| A | B | C | ((A ∧ B) → C)) | ((A → C) ∧ (B → C)) | ((A ∨ B) → C)) | ((A → C) ∨ (B → C)) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | T | T | T | T |
| 0 | 0 | 1 | T | T | T | T |
| 0 | 1 | 0 | T | F | F | T |
| 0 | 1 | 1 | T | T | T | T |
| 1 | 0 | 0 | T | F | F | T |
| 1 | 0 | 1 | T | T | T | T |
| 1 | 1 | 0 | F | F | F | F |
| 1 | 1 | 1 | T | T | T | T |
Q.28. A logical binary relation □ ,is defined as follows:
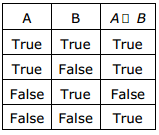
Sol : In A∧B, we have 3 entries as False, and one as True. In table, it is opposite case, so we have to negate A □ B,
moreover, we want True only when both A and B are true, so in 3rd entry (which becomes true after negation), we want both true, so
we have to negate A also.
So A ∧ B ≡ ~(~A □ B), so option (D) is correct.